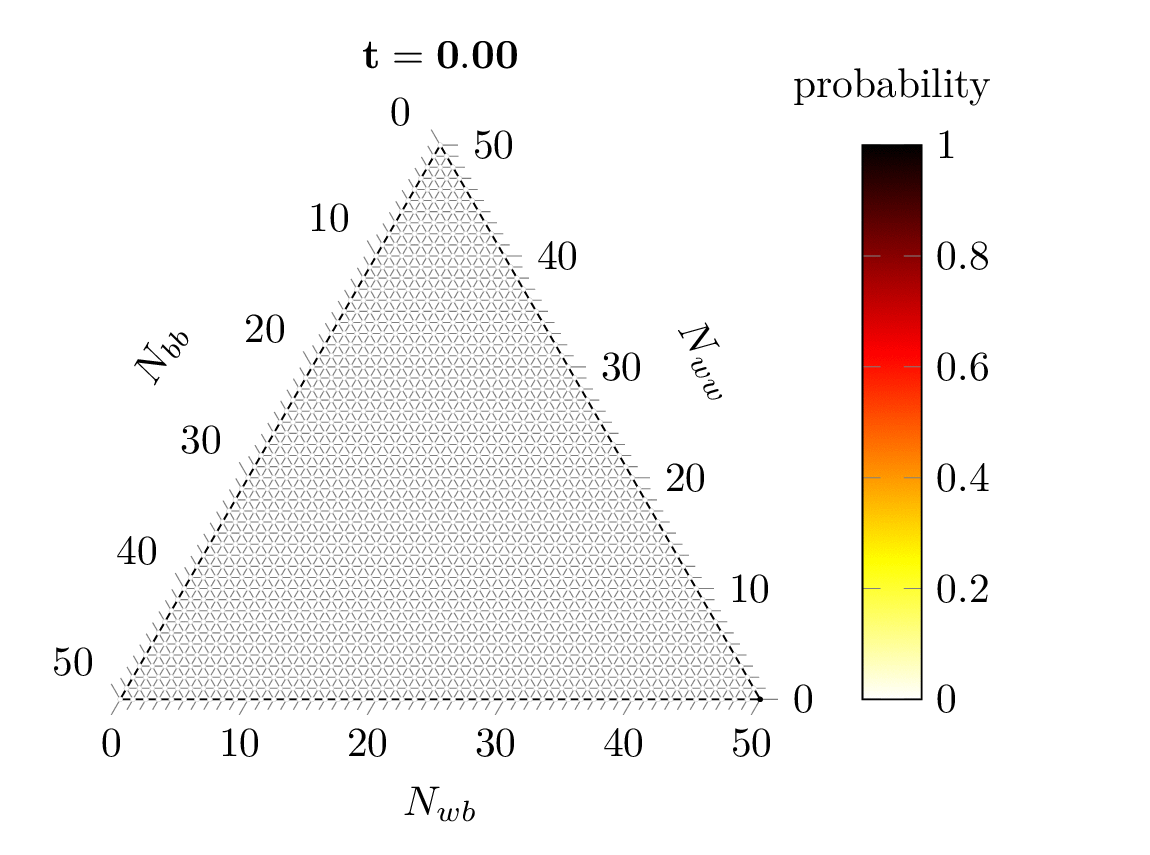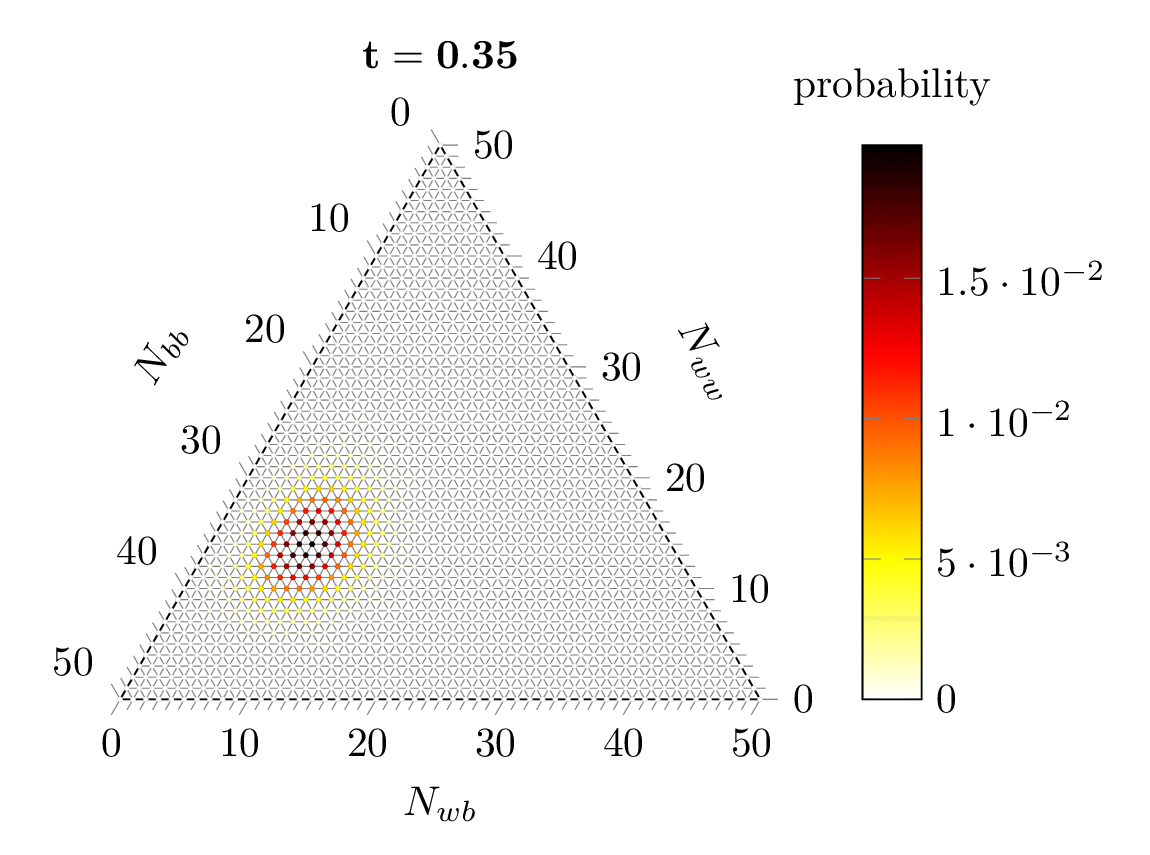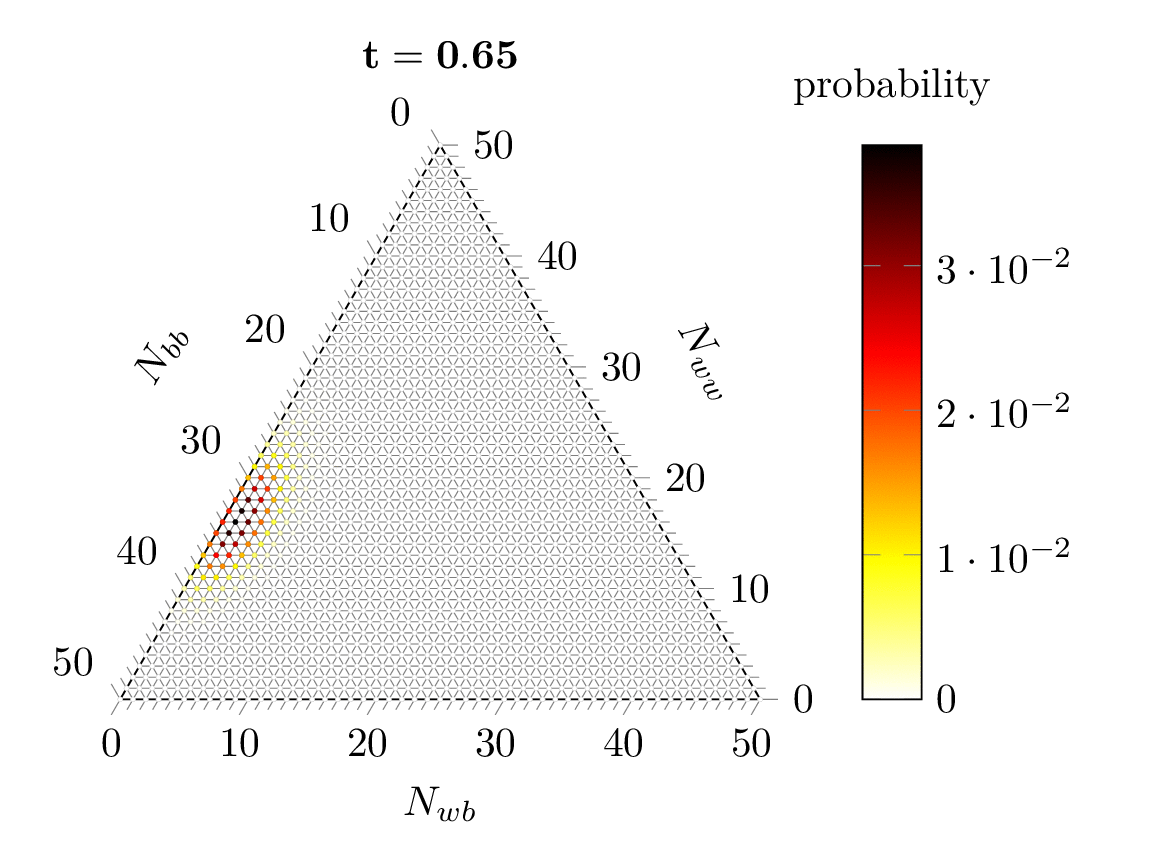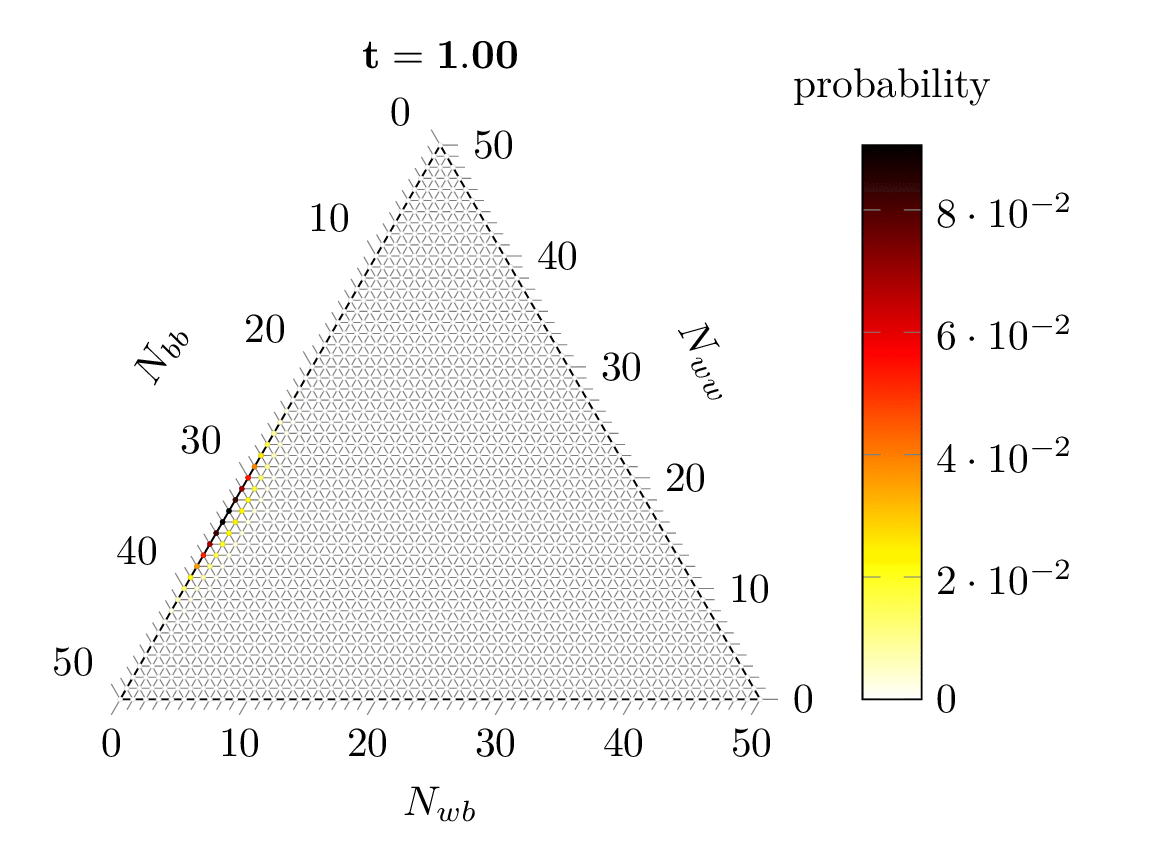
Abstract
We develop a novel method to analyze the dynamics of stochastic rewriting systems evolving over finitary adhesive, extensive categories. Our formalism is based on the so-called rule algebra framework and exhibits an intimate relationship between the combinatorics of the rewriting rules (as encoded in the rule algebra) and the dynamics which these rules generate on observables (as encoded in the stochastic mechanics formalism). We introduce the concept of combinatorial conversion, whereby under certain technical conditions the evolution equation for (the exponential generating function of) the statistical moments of observables can be expressed as the action of certain differential operators on formal power series. This permits us to formulate the novel concept of moment-bisimulation, whereby two dynamical systems are compared in terms of their evolution of sets of observables that are in bijection. In particular, we exhibit non-trivial examples of graphical rewriting systems that are moment-bisimilar to certain discrete rewriting systems (such as branching processes or the larger class of stochastic chemical reaction systems). Our results point towards applications of a vast number of existing well-established exact and approximate analysis techniques developed for chemical reaction systems to the far richer class of general stochastic rewriting systems.